신흥철 교수님의 이산수학 2강을 듣고 정리하였습니다.
논리적 동치
명제와 논리적 동치
논리적 동치(Logical Equivalence) p ≡ q
두 (합성)명제 p와 q의 진릿값이 서로 정확히 일치한다.
- p→q ≡ ¬p∨q ≡ ¬q→¬p ⇔ ¬(¬q)∨¬p ≡ q∨¬p
| p | q | ¬p | p→q | ¬p∨q | ¬q | ¬q→¬p |
|---|---|---|---|---|---|---|
| T | T | F | T | T | F | T |
| T | F | F | F | F | T | F |
| F | T | T | T | T | F | T |
| F | F | T | T | T | T | T |
논리적 동치 법칙
| 논리적 동치 | 법칙 |
|---|---|
| p∧T ≡ p p∨F ≡ p | 항등법칙(Identity Law) |
| p∧F ≡ F p∨T ≡ T | 지배법칙(Domination Law) |
| p∧¬p ≡ F p∨¬p ≡ T | 부정법칙(Negation Law) |
| ¬(¬p) ≡ p | 이중 부정법칙(Double Negation Law) |
| p∧p ≡ p p∨p ≡ p | 멱등법칙(Idempotent Law) |
| p∧q ≡ q∧p p∨q ≡ q∨p | 교환법칙(Commutative Law) |
| (p∧q)∧r ≡ p∧(q∧r) (p∨q)∨r ≡ p∨(q∨r) | 결합법칙(Associative Law) |
| p∨(q∧r) ≡ (p∨q)∧(p∨r) p∧(q∨r) ≡ (p∧q)∨(p∧r) | 분배법칙(Distributive Law) |
| ¬(p∧q) ≡ ¬p∨¬q ¬(p∨q) ≡ ¬p∧¬q | 드모르간의 법칙(De Morgan’s Law) |
| p∧(p∨q) ≡ p p∨(p∧q) ≡ p | 흡수법칙(Absorption Law) |
| p→q ≡ ¬p∨q | 합축법칙(Implecation Law) |
- 하나가 성립하면 그것의 쌍대도 항상 성립한다.
사칙연산에 비유하면 ^는 x이고 ∨는 +이다.
- 두 연산자가 같으면 결합법칙이, 다르면 분배법칙이 성립한다.
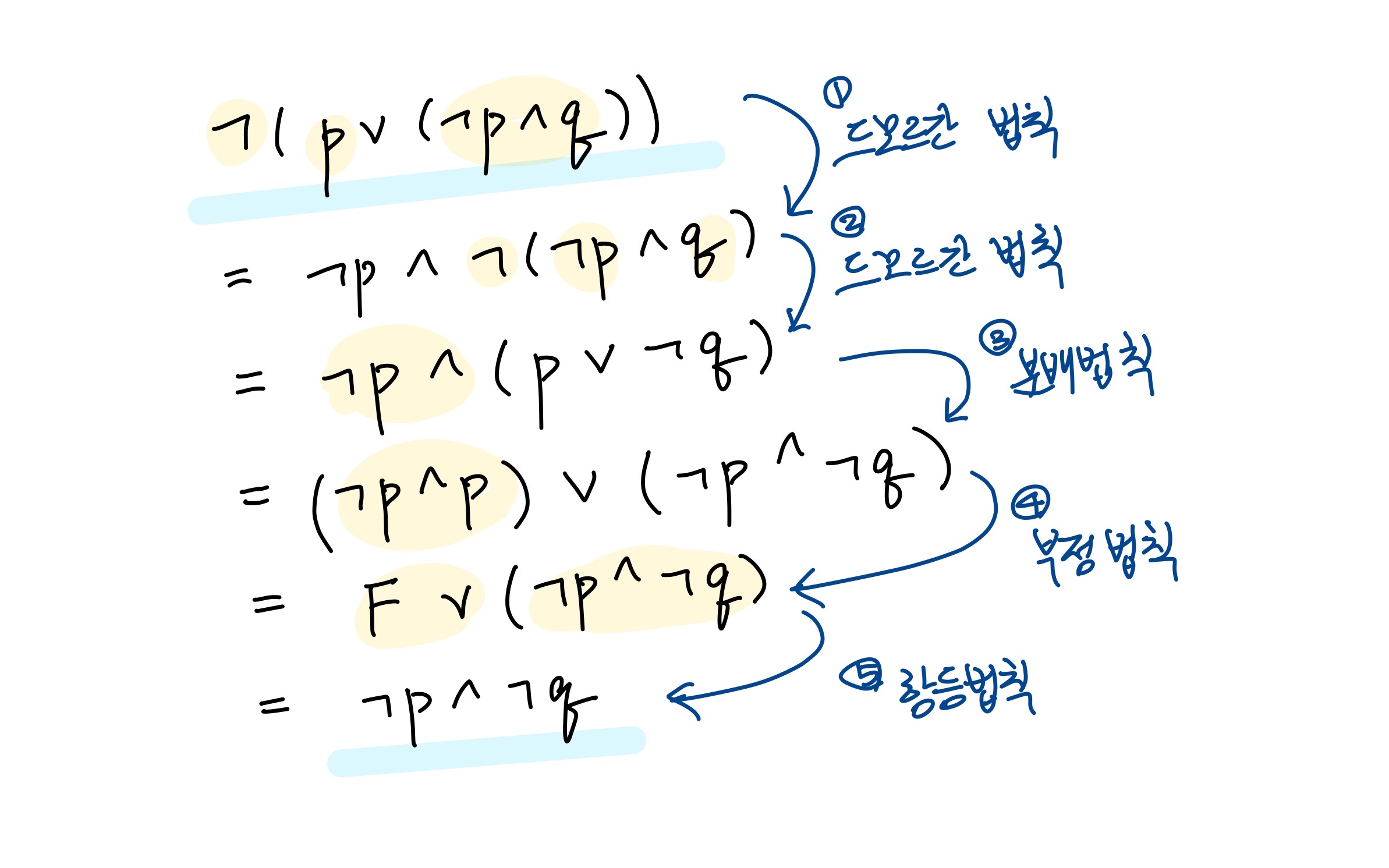
예제 1-20: ¬(p∨(¬p∧q)) ≡ ¬p∧¬q임을 증명하라.
진리표를 이용해서 두 명제가 동치된다는 것을 볼 수도 있고, 논리법칙을 이용해서 두 명제가 동치된다는 것을 볼 수도 있다. 두 방법 모두 가능하다.
우선 진리표를 이용하여 증명해보자.
| p | q | ¬p | ¬q | ¬p∧¬q | ¬p∧q | p∨(¬p∧q) | ¬(p∨(¬p∧q)) |
|---|---|---|---|---|---|---|---|
| T | T | F | F | F | F | T | F |
| T | F | F | T | F | F | T | F |
| F | T | T | F | F | T | T | F |
| F | F | T | T | T | F | F | T |
논리법칙을 이용하여 증명해보자.
예제 1-21: (p→q)∧(p→¬q)를 간략히 하라.

따라서 ¬p이다.
