신흥철 교수님의 이산수학 3강을 듣고 정리하였습니다.
변수를 포함한 명제와 한정자
명제: 참과 거짓으로 판별할 수 있는 문장 / 수식
변수를 포함한 명제: 변수의 범위(한정자, Quantifier) 지정 필요
x + 1 >= 2자체는 명제가 아니다. 그러나 변수의 범위를 어떻게 지정해주느냐에 따라서 명제가 될 수도 있고, 명제가 되지 않을 수도 있다. 예를 들어, x + 1>= 2 에서x >=1(참)이나x < 1(거짓)로 변수의 범위를 한정시켜주면 명제이지만, 범위가x < 2이면 해당 수식은 참일 수도, 거짓일 수도 있기 때문에 명제가 아니다.변수를 포함한 명제를 명제함수라고 한다. 명제함수에는 항상 한정자가 따라다녀야 한다. 만약 한정자가 없다면 명제가 될 수 없을 것이다. (참일 수도 있고 거짓일 수도 있으니까.)
한정자가 있음으로 인해서 참이면 참, 거짓이면 거짓으로 된다.
명제함수
논의영역(Universe of Discourse): D
명제에 포함된 변수 x가 속하게 될 범위
명제함수(Propositional Function): P(x)
논의영역 D에 속하는 변수 x를 포함하여 진릿값을 판별할 수 있는 문장/수식
예제 1-24: 명제함수 P(x, y)가 x = 2y일 때, P(1, 2)와 P(2, 1)의 진릿값은?
- P(1, 2): 1 != 4 -> 거짓
- P(2, 1): 2 == 2 -> 참
한정자
한정자(Quantifier)
논의 영역의 범위를 정의
전체한정자 (전칭기호, Universal Quantifier): ∀
논의 영역에 속하는 모든 값
∀xP(x): 논의영역 U에 속하는 모든 x에 대해 P(x)는 참- 논의영역의 모든 원소에 대해 만족할 경우에만 참이 됨
존재한정자 (존재기호, Existential Quantifier): ∃
논의 영역에 속하는 어떤 값
∃xP(x): 논의영역 U에 속하는 모든 x에 P(x)는 참- 논의영역의 원소 중 하나라도 만족할 경우에는 참이 됨
예제 1-26: D={x|0 < x <= 4, x는 양의 정수} 인 논의영역에 대하여, 명제함수 P(x)가 x^2 < 10일 때 다음 명제의 진릿값은?
- ∀xP(x, y): P(4) = 16 > 10이므로 ∀xP(x)은 거짓이다.
- ∃xPx(x, y): P(1) < P(2) < P(3) < 10이므로 ∃xPx()은 참이다.
예제 1-27: 실수 x, y에 대해 명제함수 P(x, y)가 x^2 < y^2일 때 다음 명제의 진리값은?
| x^2 < y^2 수식은 | x | < | y | 수식과 유사하다.??? |
∀x∃yP(x, y): 모든 x의 제곱보다 큰 어떤 y의 제곱은 존재한다.
∃x∀yP(x, y): x가 0이라면 모든 y의 값이 클 수 있다.
증명 특징
- 모든 x에 대해 참: counter example 하나 보여준다 (반증
- 어떤 x에 대해 참: 그것을 만족시키는 어떤 것 하나를 찾는다.
논리
논리와 추론
추론 (Inference)
- 어떤 명제가 참인 것을 근거로 하여 (전제, 가정명제) 다른 명제가 참임을 유도하는 방식 (결론명제)
가정/전제(Hypothesis), 결론(Conclusion)
근거가 되는 참인 명제가 가정 또는 전제가 되고, 유도되는 명제가 결론이 된다,
전제가 되는 명제는 항상 참이어야 한다. 전제가 되는 명제가 참이 아니면 추론이 될 수 없다. 추론의 시작은 전제가 참인 것부터 시작한다.
정당한 추론(유효추론)
정당한 추론: 주어진 전제(참)에 의해 유도된 결론이 참인 추론
부당한 추론: 주어진 전제에 의해 유도된 결론이 거짓인 추론
우리가 관심 있는 것은 부당한 추론이 아닌 정당한 추론이다.
예제:
- (전제) 학생들은 학교에서 공부를 한다.
- (전제) 영희는 학생이다.
- (결론) 영희는 학교에서 공부를 한다.
예제:
- 비가 오면 우산을 가지고 간다. p → q
- 비가 온다. p
- 우산을 가지고 간다. q
이 예제의 진리표는 다음과 같다.
유효추론 (p → q) & p ∴ q
| 전제 | 결론 | 전제 |
|---|---|---|
| p | q | p → q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
허위추론 (p → q) & q ∴ p
| 전제 | 결론 | 전제 |
|---|---|---|
| p | q | p → q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
논리적 추론법칙
| 법칙 이름 | 추론 법칙 | 항진 명제 |
|---|---|---|
| 논리곱(Conjunction) | p & q ∴ p∧q | 없음 |
| 선언적 부가 (Disjunctive Addition) | p ∴ p∨q | p→(p∨q) |
| 단순화 (Simplification) | p∧q ∴ p (q) | (p∧q)→p (q) |
| 긍정논법 (Modus Ponens) | p & p→q ∴ q | [p∧(p→q)]→q |
| 부정논법 (Modus Tollens) | ¬q & p→q ∴ ¬p | [¬q∧(p→q)]→¬p |
| 선언적 삼단논법 또는 소거 (Disjunctive Syllogism) | p∨q & ¬p ∴ q | [(p∨q)∧¬p]→q |
| 가설적 삼단논법 또는 추이 (Hypothetical Sylogism) | p→q & q→r ∴ p→r | [(p→q)∧(q→r)] →(p→r) |
예제 1-30: 논리적 추론법칙을 이용하여 다음 추론의 결론이 참인지 판별하시오.
- A: (¬p∨¬q)→¬r
- B: ¬r→¬s
- C: s
- ∴ q
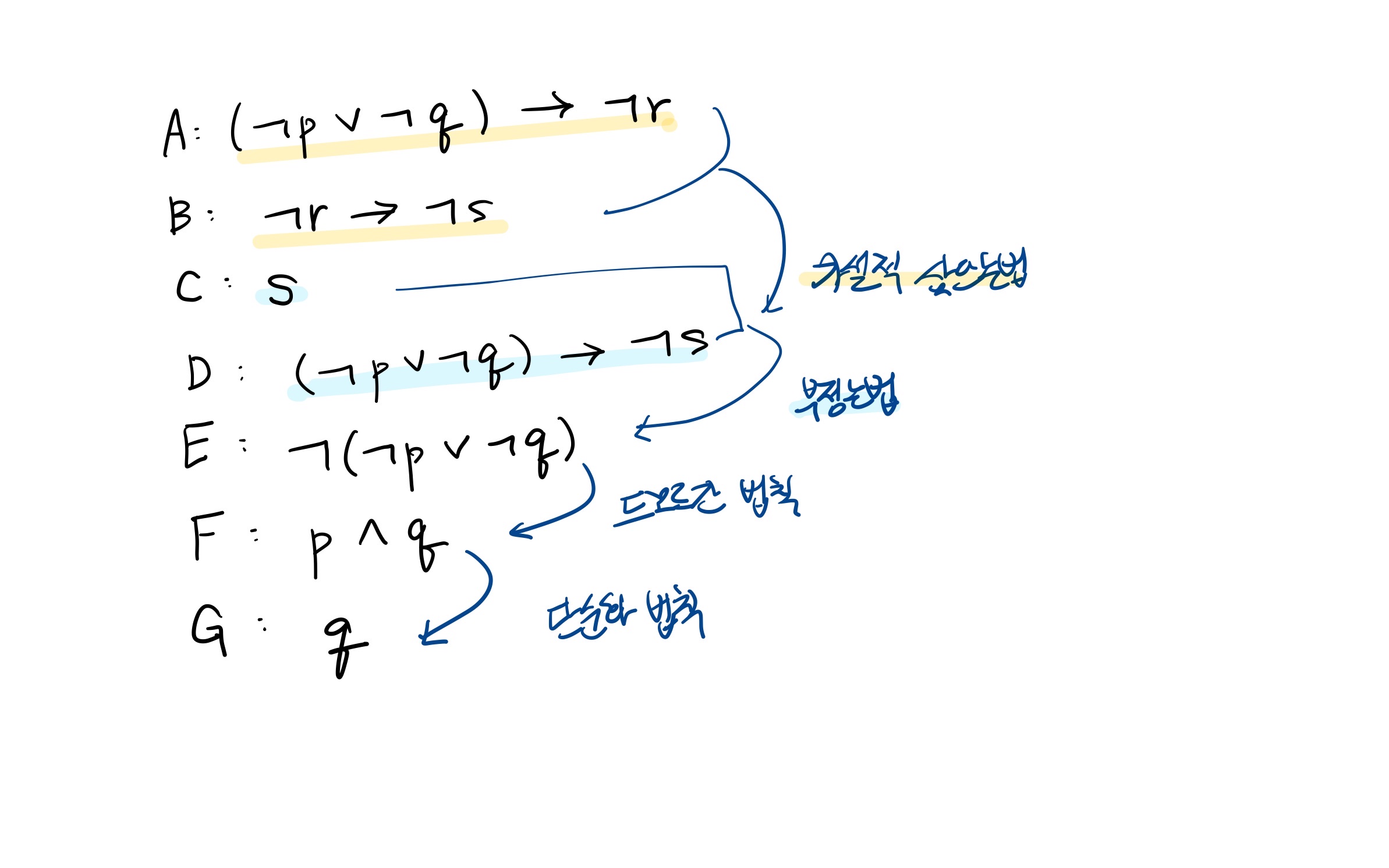
- 전제 A, B에 대해 가설적 삼단논법에 의해 D: (¬p∨¬q)→¬s
- 전제 D, C에 대해 부정논법에 의해 E: ¬(¬p∨¬q)
- 전제 E에 대해 드모르간의 법칙에 의해 F: p∧q
- 전제 F에 대해 단순화 법칙에 의해 q가 유도된다.
- ∴ q : {전제가 참이면} 추론의 결론은 항상 참이 된다.
