신흥철 교수님의 이산수학 4강을 듣고 정리하였습니다.
증명의 정의
공리 (Axiom)
- 별도의 증명 없이 참(T)으로 이용되는 명제 (무증명 명제)
- 예) 실수 a, b 에 대해 a=b이면 a + 1 = b + 1이다.
정의 (Definition)
- 논의의 대상을 보편화하기 위해 사용하는 용어 또는 기호의 의미를 확실하게 규정한 문장이나 식
- 예) ‘명제’의 정의: 참이나 거짓으로 판별할 수 있는 문장/수식
정리(Theorem)
공리와 정의((혹은 그 이전에 참으로 증명된 정리)를 통해 참으로 확인된 명제
예) 피타고라스 정리: 그 이전에 삼각형에 대한 공리와 정의를 기반으로 참임을 확인(증명).
증명(Proof)
- 하나의 명제가 참임을 확인해 나가는 과정
직접증명법(Direct Proof)
함축명제 p → q이 참이 됨을 증명하는 방법
예제2-5: 정수 n이 3의 배수면, n^3도 3의 배수인가?
p: 정수 n이 3의 배수 q: n^3은 3의 배수다. p → q: 정수 n이 3의 배수면, n^3은 3의 배수다.
n이 3의 배수이므로 n=3k(k∈Z)이고, n3=(3k) 3=27k 3=3(9k 3)이므로 n3은 3의 배수이다. ∴ 함축명제 p→q는 참(T). Q.E.D.
간접증명법(Indirect Proof)
함축명제 p → q를 다양한 형태로 변형하여 증명하는 방법
대우증명법(Proof by Contraposition)
함축명제 p→q가 대우 ¬q→¬p와 동치임을 이용하여 증명하는 방법
예제 2-14: n3이 3의 배수가 아니면, 정수 n이 3의 배수가 아님을 증명하라.
p: n3이 3의 배수가 아니다. q: 정수 n이 3의 배수가 아니다. ¬p: n3이 3의 배수다. ¬q: 정수 n이 3의 배수다.
n이 3의 배수이므로 n=3k(k∈Z)이고, n3=(3k) 3=27k 3=3(9k 3)이므로 n3은 3의 배수이다. ¬q→¬p가 참(T). ∴ 대우(동치) p→q는 참(T). Q.E.D.
모순증명법
함축명제 p→q가 ¬(p∧¬q)와 동치임을 이용하여 증명하는 방법
p→q ≡ ¬p∨ q ∵ 함축법칙 ≡ ¬p∨¬(¬q) ∵ 이중부정법칙 ≡ ¬(p∧¬q) ∵ 드모르간의 법칙
예제 2-23: 정수n이 3의 배수면, n^3도 3의 배수?
p: n3이 3의 배수가 아니다. q: 정수 n이 3의 배수가 아니다. p→q: 정수 n이 3의 배수면, n3은 3의 배수다. ¬q: n3은 3의 배수가 아니다. p∧¬q: n이 3의 배수고, n3은 3의 배수가 아니다.
n이 3의 배수이므로 n=3k(k∈Z)이고, n3=(3k) 3=27k 3=3(9k 3)이므로 n3은 3의 배수. 명제 p∧¬q이 거짓이므로 ¬(p∧¬q)은 참(T). ∴ 동치인 p→q는 참(T). Q.E.D.
반례증명법 (Proof by Counter-Example) ∃x¬P(x)
명제에 모순이 되는 예를 찾아 증명하는 방법
모든 ~에 대해서 만족한다고 할 때, 그것의 반례를 제시하여 명제가 거짓임을 증명 한정자 ∀에 대한 반증을 할 때 쓰인다.
예제 2-32: 모든 실수 a에 대해 (a+1)^2≥a^2?
반례: P(-1) = (-1 + 1)^2 = 0 < 1 = (-1)^2 모든 실수 a에 대해 (a+1)^2≥a^2이 성립하는 것은 아니다.
존재증명법(Existence Proof) ∃xP(x)
명제의 참이 되는 예를 찾아 증명하는 방법
어떤 ~에 대해서 만족한다고 할 때, 그 어떤 경우가 존재함을 제시하여 명제가 참임을 증명 한정자 ∃에 대한 증명, 무엇인가 존재하면 증명할 수 있는 방법
예제 2-35: 어떤 실수 a에 대해 (a+1)^2≥a^2?
존재: P(1) = (1 + 1)^2 = 4 >= 1=(1)^2 어떤 실수 a에 대해 (a+1)^2≥a^2가 성립한다
수학적 귀납법 (Mathematical Induction)
자연수 n에 관한 명제 p(n)이 모든 자연수 n에 대해 만족하는 것을 다음 세 단계로 증명
- 기본과정: p(논의영역 초깃값)가 참임을 증명
- 귀납가정: 임의의 k에 대해 p(k)가 참이라고 가정
- 귀납단계: 기본과정과 귀납가정을 이용해 k+1에 대해 p(k+1)이 참임을 증명
1, 2, 3, 4, … n에 대한 일력의 수식이 균일성과 규칙성을 가질 때 증명하는 방법 자연수가 아닌 경우 수학적 귀납법으로 증명할 수 없다. (실수에 대해서는 증명 X) 수학적 귀납법은 이산수학에서 큰 비중을 차지한다. 이산수학은 불연속에 대한 수학이다.
예제 2-41: n≥1일 때, n!≥2^(n-1)가 성립함을 증명

p(n): n!≥2^(n-1)일 때, 기본 가정) 초깃값 1. ∴ p(1): 1!=1≥21-1=20=1
귀납 가정) p(k): k!≥2 k-1의 성립 가정
귀납 단계) p(k+1): (k+1)!≥2(k+1)-1의 성립 증명 (k+1)!=k!(k+1)≥2 k-1(k+1) (k≥1이므로) ≥2 k-1×2=2(k+1)-1 ∴ p(k+1): (k+1)!≥2(k+1)-1 성립
∴ n≥1일 때, n!≥2 n-1가 성립한다.
예제 2-42: n-비트(bit)의 나열로 나타낼 수 있는 데이터의 최대 개수는 2 n임을 증명하시오.
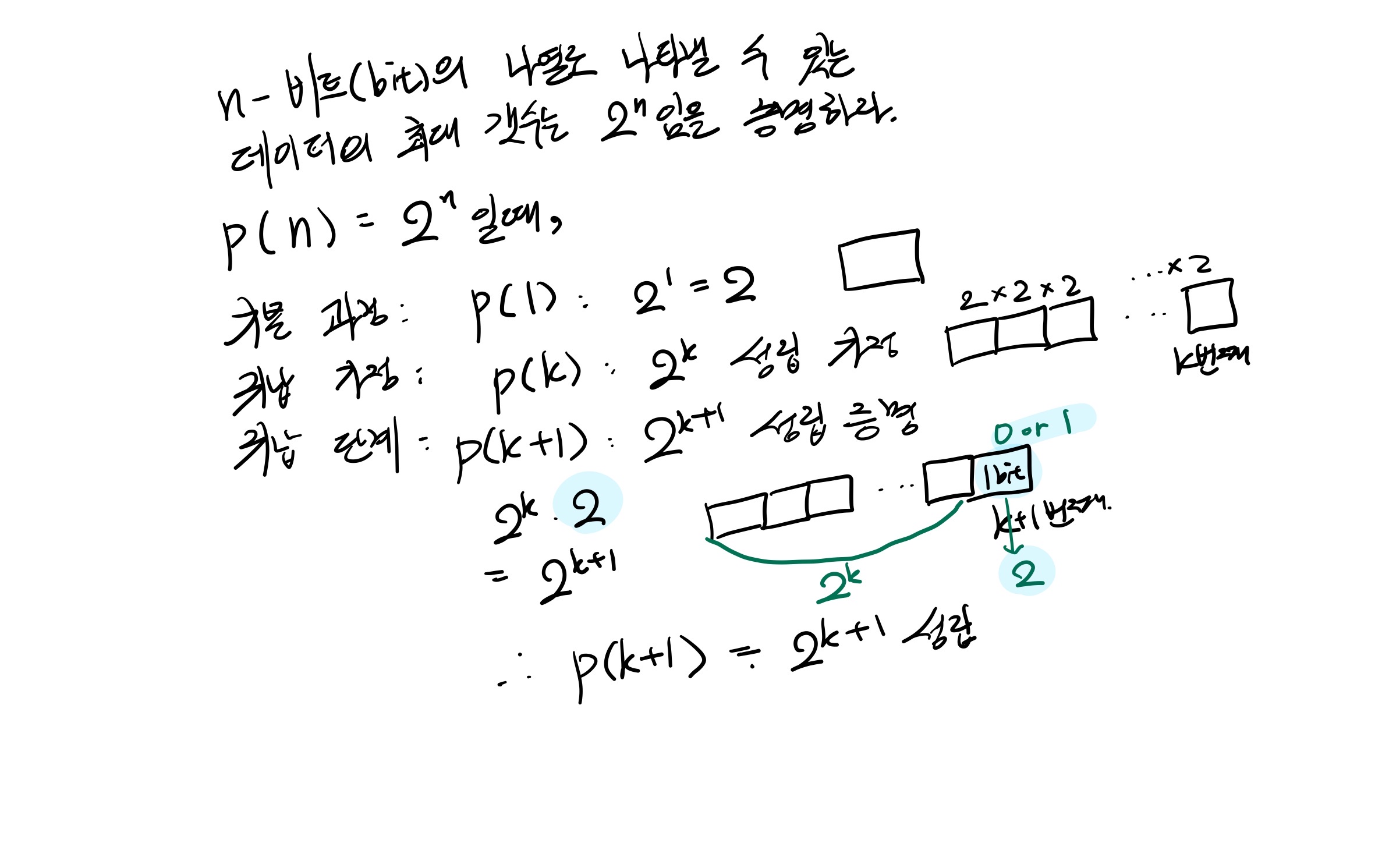
p(n): 2n일 때,
기본 가정: 초깃값 1. ∴ p(1): 21=2 (0 또는 1)
귀납 가정: p(k): 2k의 성립 가정
귀납 단계: p(k+1): 2k+1의 성립 증명 2 k+1=2×2 k는 2 k에 1비트 더 붙인 길이 2 k×2개의 데이터를 나타낼 수 있음 ∴ p(k+1): 2k+1 성립. Q.E.D.
