신흥철 교수님의 이산수학 6강을 듣고 정리하였습니다.
합집합과 교집합
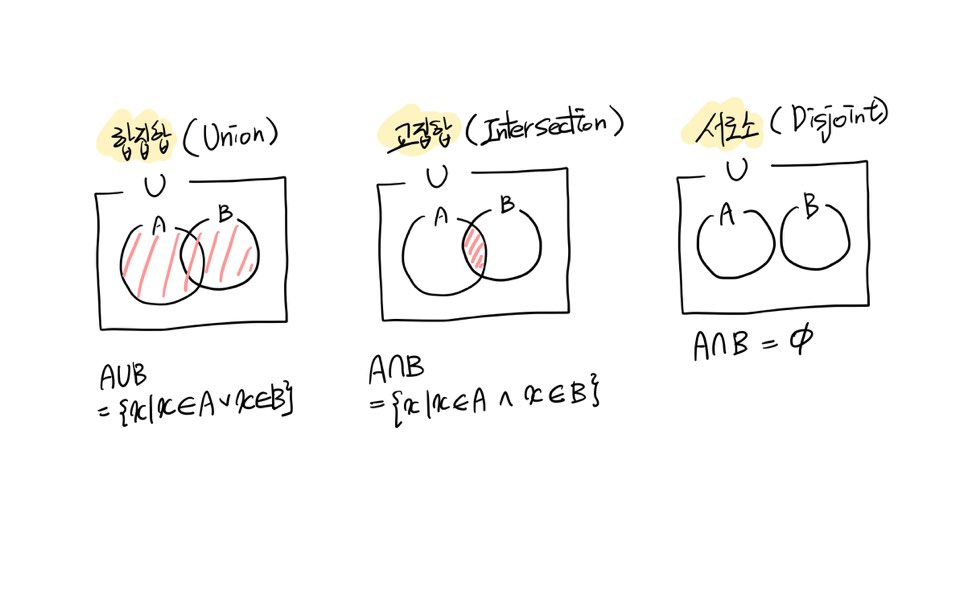
합집합(Union) A∪B
집합 A, B에 대하여, A와 B에 모두 속하거나 두 집합 중 한 집합에 속하는 원소들로 구성된 집합
A∪B={x|x∈A∨x∈B}
Q3-12. 다음 집합 A, B, C의 합집합(A∪B∪C)은?
A={a, b, c, d}, B={d, e, f, g, h}, C={c, d, e}
답: A∪B∪C = {a, b, c, d, e, f, g, h}
교집합(Intersection) A∩B
집합 A, B에 대하여, A와 B에 모두 속하는 원소들로 구성된 집합
A∩B={x|x∈A∧x∈B}
Q3-13. 다음 집합 A, B, C의 교집합(A∩B∩C)은?
A={a, b, c, d}, B={d, e, f, g, h}, C={c, d, e}
답: A∩B∩C = {d}
서로소(Disjoint)
집합 A, B에 대하여, A와 B 모두에 공통으로 속하는 원소가 하나도 없는 경우
A∩B=Ø
합집합과 교집합의 기수
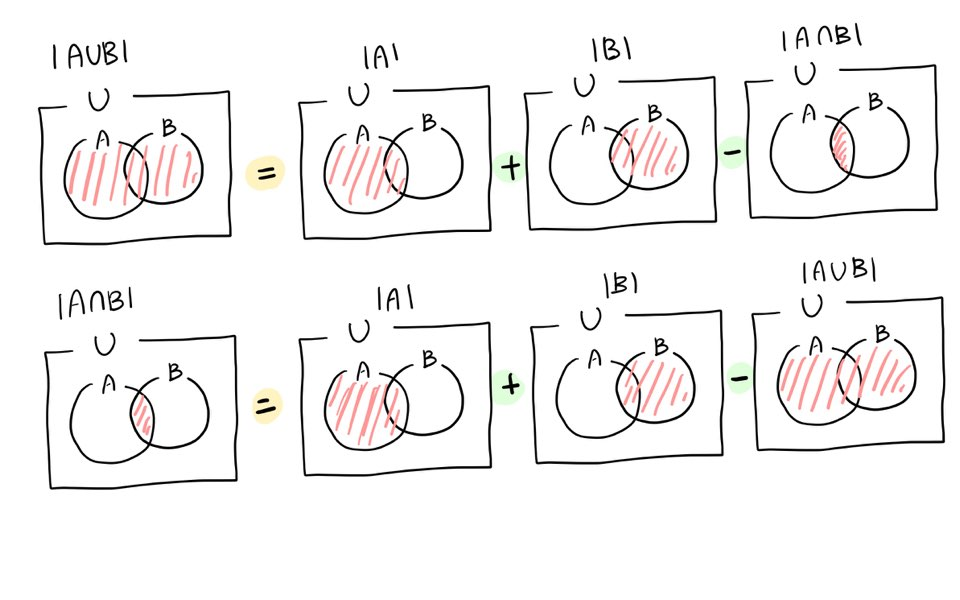
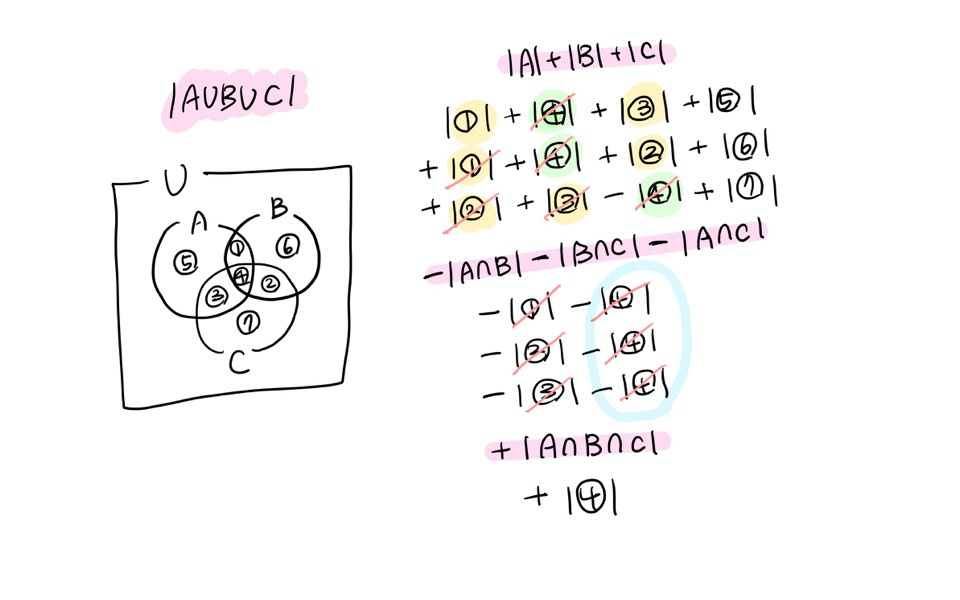
|A∪B| = |A| + |B| - |A∩B||A∩B| = |A| + |B| - |A∪B||A∩B| = Ø(서로소)인 경우,|A∪B| = |A| + |B||A∪B∪C|=|A|+|B|+|C| -|A∩B|-|B∩C|-|C∩A| +|A∩B∩C|
Q3-15. 집합 A={a, b, c, d, e, f, g}, B={e, f, g, h, i, j, k, l}, C={k, l, m, n}일 때 다음을 구하시오.
|A∪B|, |A∩C|, |A∪B∪C|
답:
|A∪B|=|A|+|B|-|A∩B|=7+8-3=12|A∩C|=0|A∪B∪C|=|A|+|B|+|C| -|A∩B|-|B∩C|-|C∩A| +|A∩B∩C| =7+8+4-3-2-0+0=14
그 외의 집합 연산
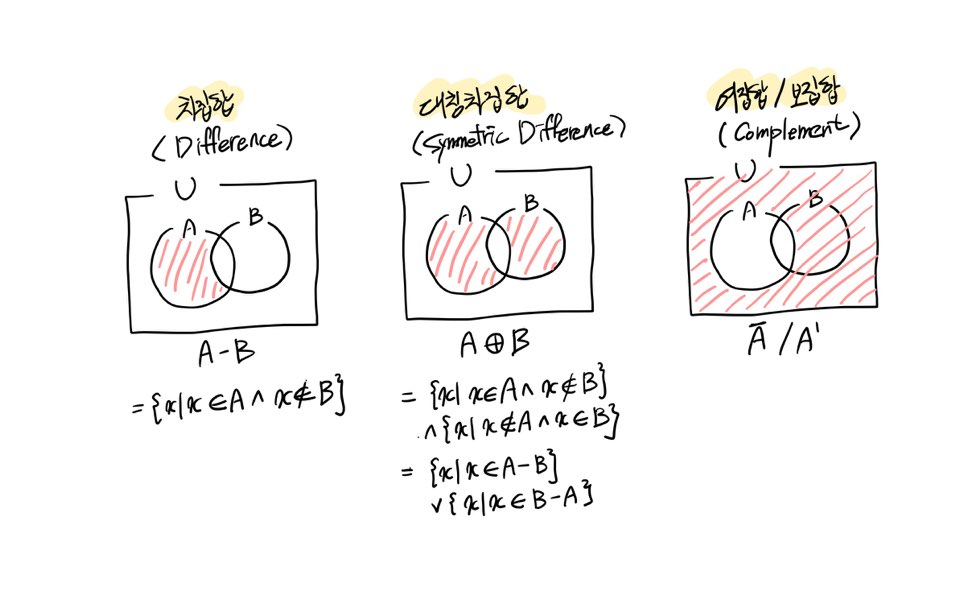
차집합(Difference) A-B
집합 A, B에 대하여, A에는 속하지만 B에는 속하지 않는 원소들로 구성된 집합
A-B={x|x∈A∧x ∉B}
Q3-16. 다음 집합 A, B에서 차집합 A-B는?
A={a,b,c,d,e,f,g,h,i,j}, B={g,h,i,j,k,l,m,n}
답: A-B={a, b, c, d, e, f}
대칭차집합(Symmetric Difference) A⊕B
집합 A, B에 대하여, A-B에 속하거나 B-A에 속하는 원소들로 구성된 집합
A⊕B
=
{x|x∈A∧x ∉B} ∨{x|x ∉A∧x∈B}=
{x|(x∈A-B) ∨(x∈B-A)}
배타적 합집합(XOR): (A-B) ∪ (B - A)
| p | q | p⊕q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
A에 속하면서 B에는 속하지 않고, B에 속하면서 A에 속하지 않는다.
Q3-19. A⊕B는?
A={a,b,c,d,e,f,g,h,i,j}, B={g,h,i,j,k,l,m,n}
답: A⊕B={a, b, c, d, e, f, k, l, m, n}
여집합 또는 보집합(Complement) Ā 또는 A’
전체집합 U에는 속하지만 집합 A에는 속하지 않는 원소들로 구성된 집합
Ā=A'={x|x∈U∧x ∉A} =U-A
Q3-20. 여집합은?
X={x|-33≤x<72, x∈R}, Y={y|y∈R}
답: X'={x|x<-33 ∨ x≥72, x∈R}, Y'={y|y∈C-R}
곱집합(Cartesian Product) A×B
- 집합 A, B에 대하여, a∈A, b∈B일 때 순서쌍 (a, b)의 집합
A×B={(a, b)|a∈A∧b∈B}|A×B|=|A|·|B|
Q3-21. A={1, 2}, B={a, b, c}에 대하여 A×B와 B×A 및 각각의 기수를 구하시오.
답:
- A×B={(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)}
- B×A={(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}
|A×B|=|A|·|B|=2×3= 6|B×A|=|B|·|A|=3×2= 6
멱집합(Power Set) P(A)
- n개의 원소를 갖는 집합 A에 대하여, A의 모든 부분집합을 원소로 갖는 집합
P(A)={B|B⊆A}|P(A)|=2**n
2**n? 원소 각각이 포함 되거나 안되거나(2)의 경우의 수.
Q3-23. A={1, 2, 3}, B={Ø, {Ø}}에 대하여 멱집합과 기수를 구하시오.
P(A)=
{Ø,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}P(B)=
{Ø, {Ø}, {{Ø}}, {Ø,{Ø}}}|P(A)|=23=8|P(B)|=22=4
