이산수학 #8강: 수의 표현

신흥철 교수님의 이산수학 8강을 듣고 정리하였습니다.

수의 종류

자연수 N

기수(base)를 b로 하는 수체계로, 양의 정수 n_b n, b∈N이고, b>1, 0≤a_i<b일 때 n=a_kb^k+a_k-1b^k-1+…+a₁b¹+a₀b⁰ (k: 자리수)

각각의 자릿수는 0이상 기수 미만: 10진수라면 각각의 자릿수는 0 이상 10미만이다.

예제 4-1. 589₁₀을 기수와 자리수로 표현하시오.

589₁₀=5×10²+8×10¹+9×10⁰

정수

양의 정수, 0, 음의 정수로 구성된 수 체계

유리수 Q

a, b∈Z(정수), a≠0일 때 b/a인 수 체계

정수부.실수부
하한항(lowest): 분모와 분자 사이에 1 이외의 공약수가 존재하지 않는 유리수 (분모와 분자가 서로소이다)
실수부(소수점 이하) 숫자들이 유한하거나 일정하게 반복됨 (예: ½=0.5, ⅓=0.333…)

무리수 I

a, b∈Z, a≠0일 때 b/a로 표현할 수 없는 수 체계

실수부(소수점 이하) 숫자들이 무작위로 나열됨
예: 루트2

실수 R (=N∪Z∪Q∪I)

자연수, 정수, 유리수, 무리수를 포함하는 수 체계

r∈R, b∈N이고, b>1, 0<a_i<b일 때

r =a_kb^k+a_k-1b^k-1+…+a₁b¹+a₀b⁰ +a_-1b^-1+a_-2b^-2+… (k: 자리수)

예제4-5. 345.734₁₀을 기수와 자리수로 표현?

345.73410=3×10²+4×10¹+5×10⁰ +7×10^-1+3×10^-2+4×10^-3

복소수 C

x² = -1 를 포함하는 수 체계

c=a+bi(a: c의 실수부, b: c의 허수부)로 표현하되, 연산은 아래와 같음

(a+bi)+(c+di)=(a+c)+(b+d)i
(a+bi)·(c+di) = (ac+adi)+(bci+bdi²) = (ac-bd)+(ad+bc)i

예제 4-6. 복소수 3+6i와 12i에 대해 합과 곱은?

(합) (3+6i)+12i=3+18i
(곱) (3+6i)×12i=36i+72i2= (-72)+36i

수의 연산

수의 닫힘 성질 (closure)

어떤 수 체계에 속한 원소들에 대해 연산한 결과가 수 체계에 속하게 되면 연산에 대해 닫혀있다고 한다.

	덧셈	뺄셈	곱셈	나눗셈
자연수(N)	○	×	○	×
정수(Z)	○	○	○	×
유리수(Q)	○	○	○
무리수(I)	×	×	×	×
실수(R)	○	○	○	○
복소수(C)	○	○	○	○

수의 합과 곱에 대한 특징

교환법칙: x+y=y+x, xy=yx
결합법칙: (x+y)+z=x+(y+z), (xy)z=x(yz)
분배법칙: x(y+z)=xy+xz
합에 대한 항등원: 0
곱에 대한 항등원: 1
합에 대한 역: -a
곱에 대한 역: 1/a

예제4-7. 9의 합과 곱에 대한 역을 구하시오.

(합)9+a=0 ∴a=-9
(곱) 9×a=1 ∴a=1/9

합의 표시 ∑xi

일정한 규칙으로 나열된 값의 합 (i: 합의 색인)
x₁+x₂+x₃+…+x_i+…+x_n-1+x_n

곱의 표시 ∏xi

일정한 규칙으로 나열된 값의 곱(i: 곱의 색인)
x₁× x₂×x₃×…× x_i×…× x_n-1×x_n

나누기 연산 d|n

정수 n을 d로 나누어 몫 q를 구하는 연산 또는 n=dq를 만족하는 정수 q를 구하는 연산

d|n: d로 n을 나눈다. (d≠0)
d∤n: d는 n을 나누지 못한다.
q: 몫(quotient)
d: n의 약수(divisor) 또는 인수(factor)
n: d의 배수

나누기 연산의 규칙(a, b, c, d, m, n은 정수)

d|m이고 d|n이면 d|(m+n)
m=dk, n=dl (k, l∈Z) ∴m+n=dk+dl=d(k+l)
d|m이고 d|n이면 d|(m-n)
m=dk, n=dl ∴m-n=dk-dl=d(k-l)
d|m이면 d|mn
m=dk, mn=dkn=d(kn)
a|b이고 b|c이면 a|c
b=ak, c=bl c=akl=a(kl)

나머지 연산 n mod d

정수 n을 d로 나누어 나오는 몫 q와 나머지 r이 있을 때, r을 구하는 연산 또는 n=dq+r을 만족하는 정수 r을 구하는 연산

n mod d = r
q: 몫(quotation)
d: n의 약수(divisor) 또는 인수(factor)
n: d의 배수
r: 나머지(remainder), 0≤r<d
n mod d = 0 ⇔ d|n

수 체계

10진수(Decimal Number)

기수를 10으로 하는 수 체계, 0에서 9사이의 숫자를 이용해 수를 표현

정수 n에 대해 (k>0, 0≤a≤9)
n₁₀
= a_ka_k-1 …a₁a₀
= a_k10^k+a_k-110^k-1+…+a₁10¹+a₀10⁰
실수 n에 대해 (k,l>0, 0≤a≤9)
n10
= a_ka_k-1 …a₁a₀a_-1a_-2…a_-l …
= a_k10^k+a_k-110^k-1+…+a₁10¹+a₀10⁰ +a_-110^-1+a_-210^-2+…+a_-l10^-l+…

2진수(Binary Number)

기수를 2로 하는 수 체계, 0과 1을 이용해 수 표현

실수 n에 대해 (k,l>0, a=1 또는 0)
n₂
= a_ka_k-1 …a₁a₀a_-1a_-2…a_-l …
= a_k2^k+a_k-12^k-1+…+a₁2¹+a₀2⁰ +a_-12^-1+a_-22^-2+…+a_-l2^-l+…

8진수 (Octal Number)

기수를 8로 하는 수 체계, 0에서 7사이의 숫자를 이용해 수를 표현

실수 n에 대해 (k,l>0, 0≤a≤7)
n8
= a_ka_k-1 …a₁a₀a_-1a_-2…a_-l …
= a_k8^k+a_k-18^k-1+…+a₁8¹+a₀8⁰ +a_-18^-1+a_-28^-2+…+a_-l8^-l+…

16진수 (Hexadecimal Number)

기수를 16으로 하는 수 체계, 0에서 9와 A(10)에서 F(15) 사이의 숫자를 이용해 수를 표현

실수 n에 대해 (k,l>0, 0≤a≤9 또는 A≤a≤F)
n16
= a_ka_k-1 …a₁a₀a_-1a_-2…a_-l …
= a_k16^k+a_k-116^k-1+…+a₁16¹+a₀16⁰ +a_-116^-1+a_-216^-2+…+a_-l16^-l+…

예제4-15. 9B.FE316을 기수와 자리수를 이용해 풀어 쓰시오.

9B.FE3₁₆

= 9×16¹+B×16⁰ +F×16^-1+ E×16^-2+3×16^-3

= 9×16¹+11×16⁰ +15×16^-1+14×16^-2+3×16^-2

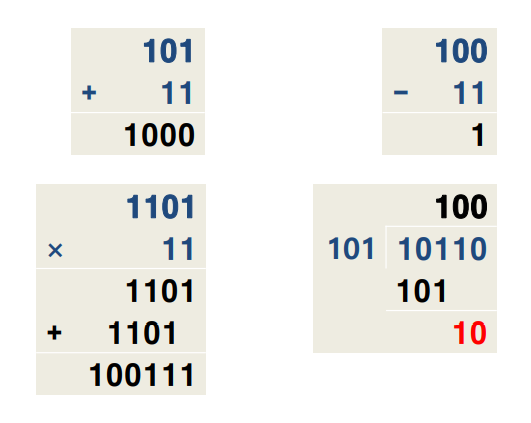
예제 4-17. 다음 2진수를 연산하시오.

101+11, 100-11, 1101×11, 10110÷101

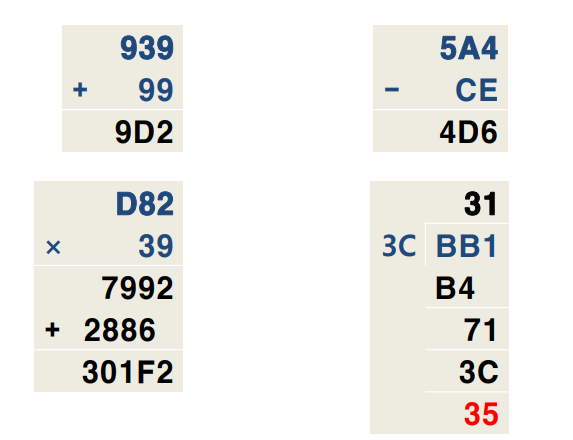
예제 4-19. 다음 16진수를 연산하시오.

939+99, 5A4-CE, D82×39, BB1÷3C

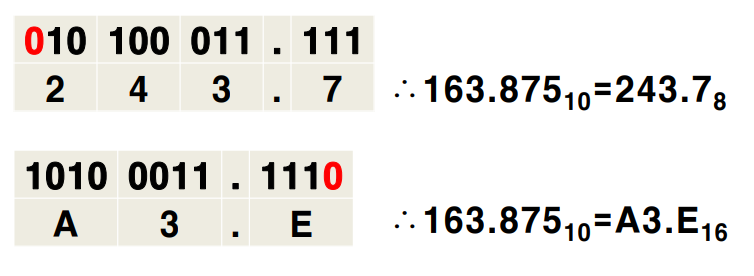
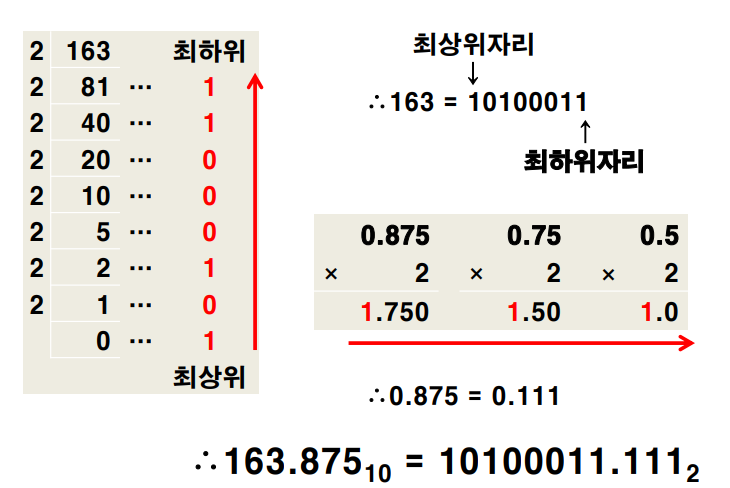
예제 4-20. 10진수 163.875를 2진수로 변환

예제 4-20. 10진수 163.875를 8, 16진수로 변환

163.87510 = 10100011.1112